Information

• Please register in RWTHonline to get access to the Moodle room.

Course Material

• Lecture Notes (pdf).

• See Moodle room for further material.

Content

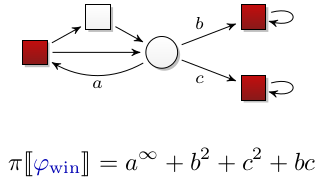
Semiring provenance is a successful approach, originating in database theory, to provide detailed information on how atomic facts combine to yield the result of a query or the truth of a logical statement. This is achieved by defining semiring semantics for various logics, where we evaluate logical statements not just by true or false, but by values in some comutative semiring. In this course, we introduce semiring semantics and study its properties and applications for provenance analysis of logic and games. More specifically, we may cover these topics:

• Algebraic and order-theoretic foundations of commutative semirings.
• Semiring semantics for database query languages (relational algebra, datalog,...) and logics (first-order logic, modal logics, fixed-point logics, ...), with applications to confidence scores, cost computation, and access control.
• General provenance analysis by semirings of polynomials and formal power series.
• Model-theoretic and algorithmic properties of semiring semantics.
• Strategy analysis in finite and infinite games.

Learning Goals

• Commutative semirings and their algebraic properties. Semiring interpretations. Semiring valuations of logical statements, database queries, and positions in games. Fundamental facts about the model theory and complexity of semiring valuations.
• The student will be able to evaluate logical statements in various semirings, to track which combinations of basic facts are responsible for the truth of a complex statement, to apply semiring valuations in the analyis of issues such as confidence, cost, access control, proof counts, or repairs, and to analyse the available strategies in games via semiring valuations.

Classification

• Informatik (M.Sc.) / Theoretische Informatik
• Mathematik (M.Sc.) / Angewandte Mathematik

Exam

Exam information will be announced during the semester.

Prerequisites

• Mathematical Logic

Contact

Erich Grädel